Python Sudoku Solver

Sudoku is a logical, number-based puzzle , which have been popular in newspapers and puzzle books since the 19th century. The aim is to fill a 9 x 9 grid with the numbers 1 – 9 , such that every row, every column and each 3 x 3 squares contain the digits only once.

The Code…

• The only package imported for this program is “numpy” simply so that the sudoku is outputted in a readable format as a matrix, and not a list of elements.

• The Sudoku must be translated into a 2-Dimensional Array such that the digits are entered, and where there is an empty space to be filled, a “0” is entered. For example:

grid = [
		[5,3,0,0,7,0,0,0,0],
		[6,0,0,1,9,5,0,0,0],
		[0,9,8,0,0,0,0,6,0],
		[8,0,0,0,6,0,0,0,3],
		[4,0,0,8,0,3,0,0,1],
		[7,0,0,0,2,0,0,0,6],
		[0,6,0,0,0,0,2,8,0],
		[0,0,0,4,1,9,0,0,5],
		[0,0,0,0,8,0,0,7,9]
							]

• Two helper functions will be created for the entire Sudoku solver program!

Function 1: “possible”

• First a function called “possible” is created, whose job will be to check whether it is possible to place a number at a given row-column intersection
• The “x” and “y” coordinates in the code refers to the diagram below where “x” are the rows, and “y” are the columns

• The function checks that an input number “n” does not already exist in the row, the column OR the 3 x 3 square sub-grid
• If the number does not exist in either of the row, column or square 3 x 3 grid –> then the function returns TRUE

Function 2: “solve”

• This function is ultimately what “solves” the sudoku puzzle (as the name suggests…)

• Starting from element 0 in the row and column, the function checks if the element is equal to “0”, which means it is blank.
• Next, it iterates through each of the digits from 1 to 9 (“n”), calling the helper Function 1 (“possible”) to see if this “n” value would fit in that correct row-column intersection
• If the “possible” function returns TRUE, then it goes ahead and places the value of “n” into the grid and this has reduced one of the “0”s in the grid, since one blank number is filled in

Recursion within the program

• The recursive nature of this program is where the function “solve” is called within the function “solve” (it was difficult to understand this at first, but makes sense since we would like to keep solving the blank elements in the grid until there are no more blank items left)
• Definition: “recursion” = a programming technique using function or algorithm that calls itself one or more times until a specified condition is met

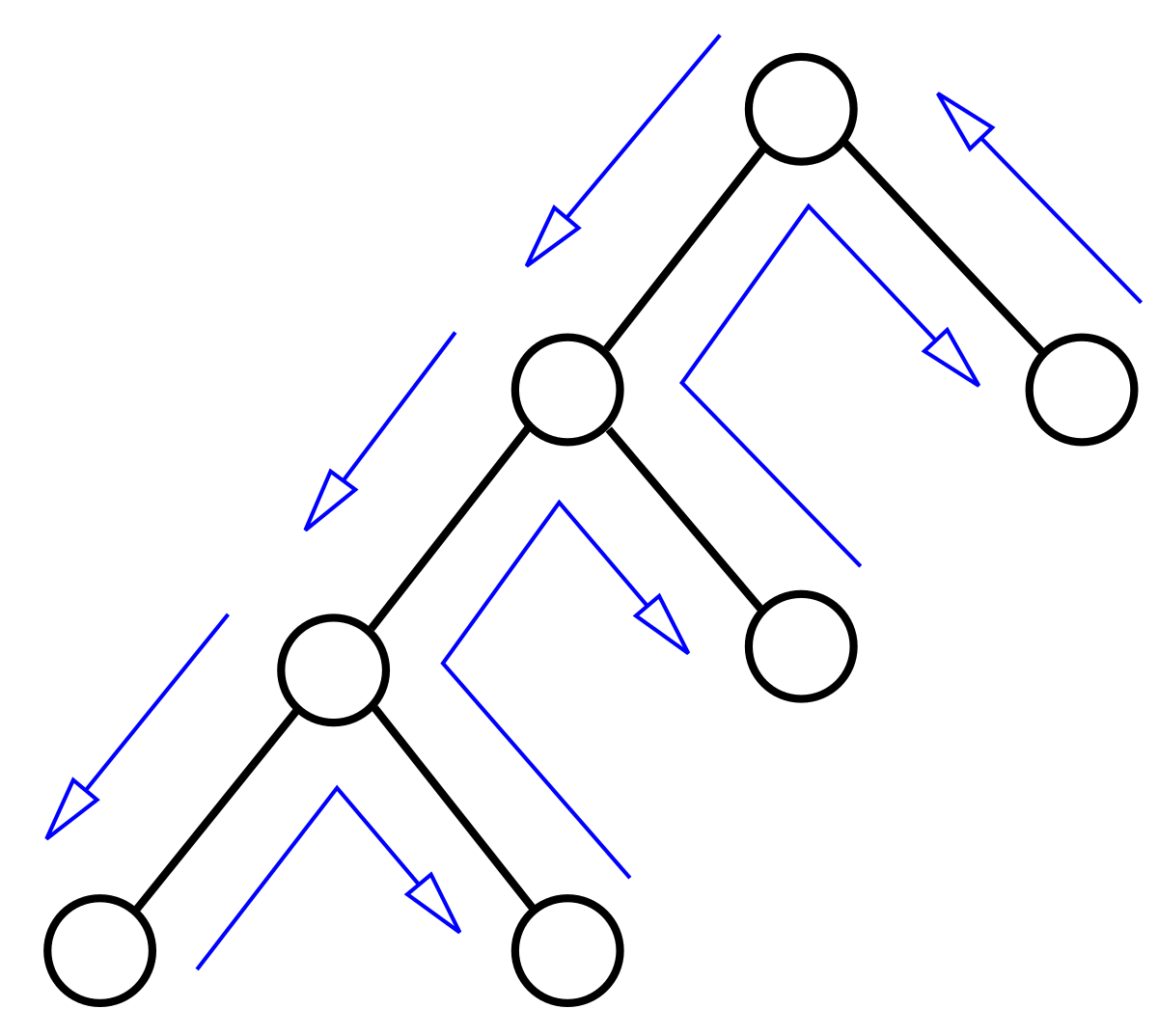
Technique used: Backtracking

Backtracking is an algorithmic technique in Computer Science in which a complete solution is built incrementally, where different values are tried one-at-a-time, and if the value leads to a dead-end, it is removed and we “backtrack” to the previous stage.

In context, for the Sudoku algorithm, we try filling each digit one-by-one. If we find out that the current digit does not lead to a solution, it must be removed and we go back to the previous stage and try the next digit. This is the backtracking step. (see diagram –>)

Come up with a partial solution –> attempt to extend it –> if you get the solution, perfect! –> if not, backtrack and try a different solution higher up –> repeat and try again.

An example to illustrate this is in a maze. If you want to get from Start to Finish, you try a few paths. Imagine you try one path, and it leads to a dead-end. What do you do to get to the Finish?

You backtrack to the last point where you were on track, and try another route to see if this gets you closer to the Finish.

Similarly, this process is adapted to this Sudoku algorithm, as well as other examples: crosswords, verbal arithmetic, the eight queens puzzle and many more.

Complete!

And that’s the summary of the Sudoku solver program! I tested the program by going to the website “https://sudoku.com/evil/” and choosing the most difficult Sudoku. After a second of thinking, the program outputted the correct solution 🙂

Feel free to have a go with the program below –> enter your Sudoku to be solved in the grid (each element is separated by a comma, and the blanks are represented by a “0”).

References:

• Computerphile video: Thank you to Professor Thorsten Altenkirch & Sean Riley
• What is backtracking?
• GeeksForGeeks Backtracking Algorithm