This problem is based in the City of Königsberg in the 18th century. The legend goes that there was a competition within the citizens as to whether anyone could walk around the city crossing the seven bridges linking the different parts of the city exactly once. There were a few citizens claiming they had done which raised speculation, and people were wondering how it was possible.

In Figure 1 above, you can see a rough map outlining the bridges to cross between the land masses. Why don’t you have a go to start from one bridge and visit every landmass by crossing each bridge ONLY ONCE? See if you can your find your solution…
[Enter Leonard Euler…]
You may be shocked to see that the famous mathematicians Leonard Euler is also involved in solving this problem!
The way that Euler went about solving this problem is that he decomposed the map of the city to a diagram (right diagram on Figure 2), and more specifically a graph! He wrote (what is thought to be) the first ever paper on Graph Theory.

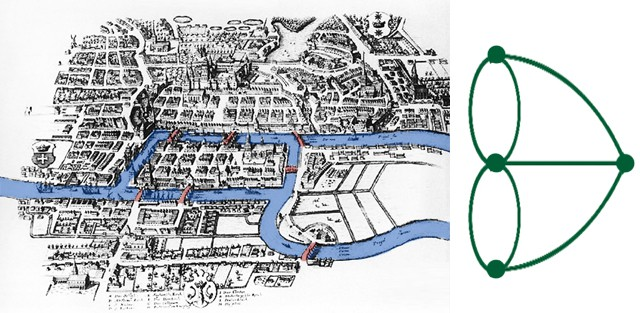
Here he represented the 4 land masses as 4 nodes (or dots…), and the bridges represented the edges of the graph (or lines joining the dots…) The aim is to see whether you can start at one of the vertices, and trace your way round the graph WITHOUT having to go over any edges twice.
Drawing a House (sub-problem)
I’m going to pause with the explanation of The Bridges of Königsberg problem briefly to fill you in with another famous graph theory problem…
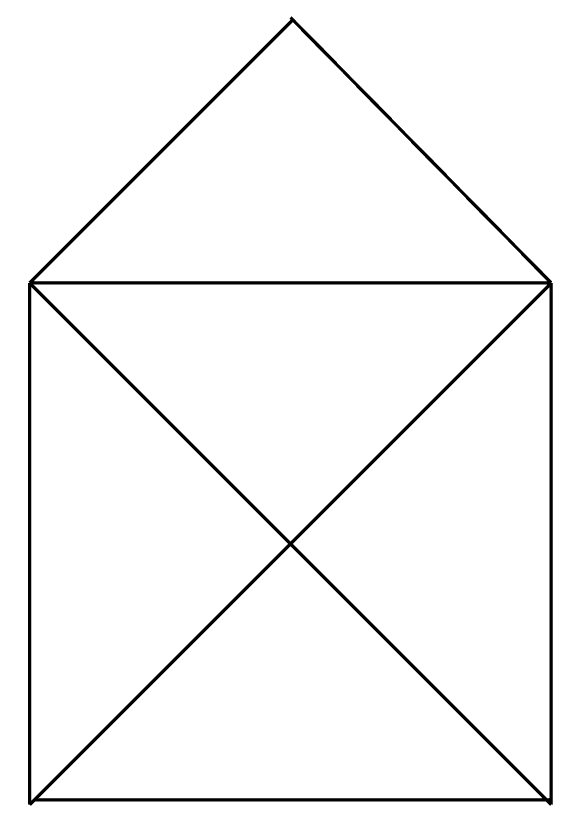
The question is: “Given the shape of a simple house (Figure 3) with a cross inside of it, can you re-draw the same shape with a pen WITHOUT lifting it up?”
A few terminologies: the degree of a node = how many edges are connected (incident) to it. So for example, for the Figure 3 house, the degree of each node is shown in Figure 4:

An Euler Path is a path taken through a graph that uses each of its edges exactly once. For an Eulerian Graph specifically, you MUST have an even number of edges coming out of each node (i.e. all nodes must have an even degree). The reason to understand this is because when you ENTER a node by an edge, you must also LEAVE the node by another edge and thus we must have an even degree at each node).
If you are prepared to start and end at different vertices, the graph can have at most two nodes with an odd degree. This graph is known as a Semi-Eulerian Graph.
Therefore, all the other nodes (apart from the 2 with the odd degree) must have even degree AND the number of nodes with odd degree is either 0 or 2 (since the sum of all the nodes in a graph is always even).
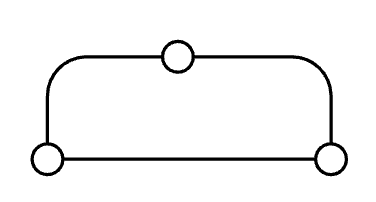
Further to this, if there are 0 nodes with an odd degree in the graph, the path can start and end at any node… this is known as an Euler circuit! e.g. Figure 5
Therefore, with these concepts above you can deduce that the Drawing the House problem MUST have an Euler path (since from Figure 3 we have at two nodes with odd degree which is allowed as stated above…) BUT it means hat the pen must start and end at the bottom two nodes, since they are the only nodes with odd degrees.
Back to Königsberg…
Now that we have a background into Euler paths and the degree of a node, we can go through Euler’s solution to The Bridges of Königsberg.
Having described the rules of an Eulerian and Semi-Eulerian graph above, in our case of The Bridges of Königsberg, each vertex has an odd number of edges coming out of it (= odd degree). In Figure 6 below, Node A has degree 5, Node B has degree 3, Node C has degree 3 and finally Node D has degree 3 as well. (5 and 3 are both odd numbers).
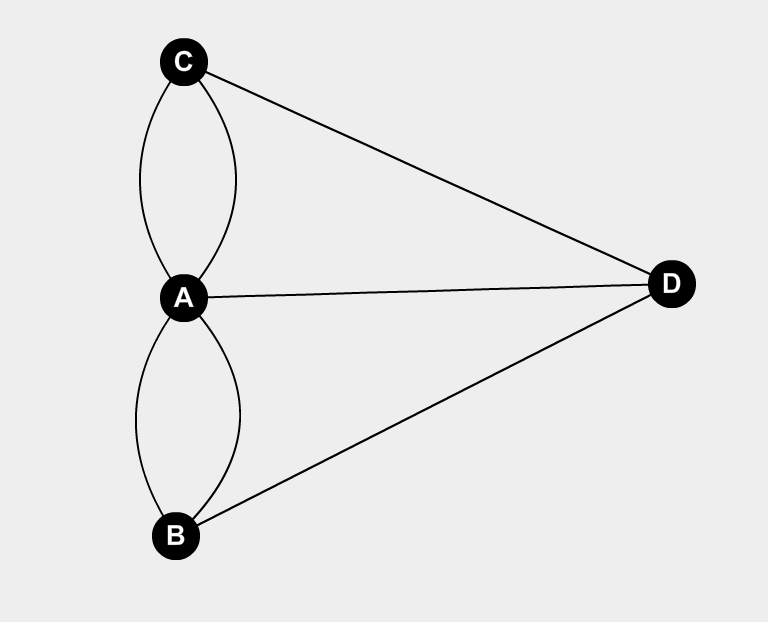
Therefore, Euler was able to conclude that since all the nodes have odd degrees, the The Bridges of Königsberg graph is NOT an Eulerian nor a Semi-Eulerian graph. Hence, there is NO WAY to walk around the city of Königsberg crossing each bridge only once… the problem was IMPOSSIBLE! (so all those citizens who claimed they were able to do it were wrong!)
Quick treat (quiz!) for those of you who love graph theory
Which of the following graphs in Figure 7 are Eulerian graphs, Semi-Eulerian graphs or neither?
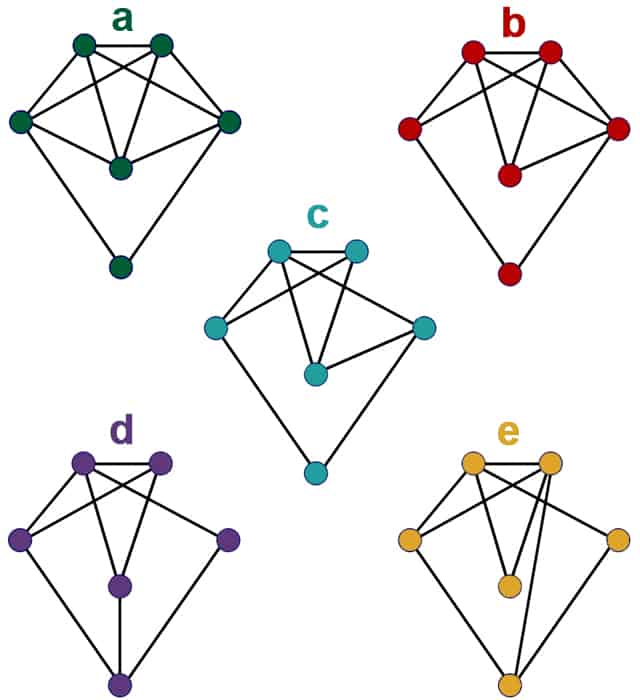
(HINT: Look at the number of edges coming out of every node, and scroll up to recall the rules of Eulerian and Semi-Eulerian Graphs]
(Click here to find the Answers to the Quiz:)
Power of Mathematics and Computer Science!
A simple to state problem has now led to great advancements in modern day, since graph theory drives the computation behind transport systems, electricity networks, social networks (FaceBook) and can even model the entire Internet with its billions of webpages linked together in a graph!
Maths and Computer Science are inextricably linked, and what amazes me is how the solution of a problem decades old can lead to revolutionary changes in the world in the future.
References:
With thanks to:
- https://www.mathscareers.org.uk/bridges-of-konigsberg-and-graph-theory/
- https://siawyoung.com/drawing-a-house
- TLMaths YouTube channel for the A-Level Maths video which introduced me to Graph Theory
Answers to the QUIZ:
(a) EULERIAN graph: Every node has even degree (even number of edges coming out of it)
(b) SEMI-EULERIAN graph: has two nodes with odd degree
(c) NON-EULERIAN graph: has four nodes with odd degree (therefore not semi-eulerian nor eulerian)
(d) NON-EULERIAN graph: has three nodes with odd degree
(e) SEMI-EULERIAN graph: has two nodes with odd degree
